Mean field analysis

A general behavior of rule B2/S2345678 can be well described by a mean field polynomial and its fixed points (see fig. 1), as follow:

pt+1 = 28pt2qt7+28pt3qt6+56pt4qt5+70pt5qt4+56pt6qt3+28pt7qt2+

         8pt8qt+pt9.

High densities of domains dominated by state 1 correspond to p=0.9196 to p=1 (also we can consider p=0.6598 to p=0.7252, all they are stable fixed points). Interesting behavior can be found in extreme unstable fixed points when p=0.00036 to p=0.001. Thus unstable fixed points may represent gliders and small oscillators as show fig. 2.

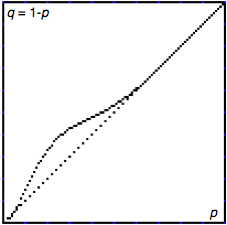
Fig. 1 Mean field curve for B2/S2345678.

Fig. 2 Snapshots showing activity of gliders and oscillators in B2/S2345678. (Left) initial condition with a density of 0.004 into a lattice of 300 x 300. (Right) show its evolution late of 65 times as nucleation phenomenon covering the evolution space quickly with a population of 23,802 live cells, and some gliders and oscillators survival in this time even.

Fig. 3 Basic periodic structures in B2/S2345678: (a) glider period one, (b) oscillator period one, (c)flip-flop, and (d) still life configuration.

Basic periodic structures in B2/S2345678

Minimal localizations, or basic periodic structures, in rule B2/S2345678 include gliders, oscillators, flip-flops, and still life (stationary localization) configurations (fig. 3).

Indestructible pattern in B2/S2345678

A relevant characteristic was that the rule B2/S2345678 supports indestructible patterns, which can not be destroyed from any perturbation, they belong to the class of stationary localizations, still lives. The minimal indestructible pattern is show in fig. 3d. More heavier, in a number of live cells, patterns are provided in fig. 4.

In CA rule B2/S2345678 one can setup colonies of the indestructible structures as sets of block patterns, which are capable for resisting internal and external perturbations, see examples in fig. 4. The indestructible patterns symbolize a precipitation in CA development. We use these patterns to architecture channels, or wires, for signal propagation.

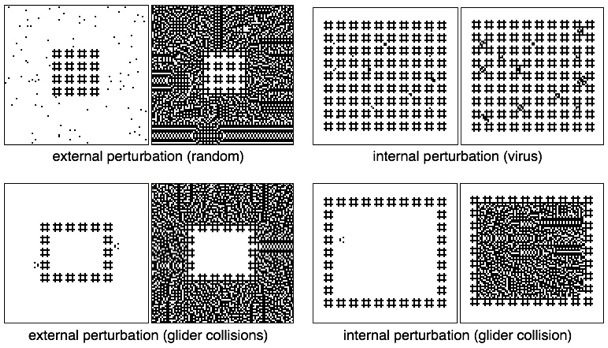
Fig. 4 Indestructible Still Life colonies `tested' by internal and external perturbations. Each pair of snapshots represents an initial condition (on the left) and a final, i.e. stationary, configuration (on the right).

Computing with propagating patterns

We implement computation with patterns propagating in the Life rule B2/S2345678 is follows. A computing scheme is build as channels, geometrically constrained by Still Life indestructible blocks, and T-junctions (T-junction based control signals were suggested also in von Neumann (ref. 1966) works), between the channels. Each T-junction consists of two horizontal channels A and B (shoulders), acting as inputs, and a vertical channel, C, assigned as an output (fig. 5).

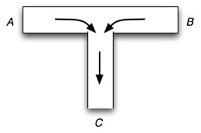
Fig. 5 T-junction system.

Boolean values are represented by gliders, positioned initially in the middle of channel, value 0 (fig. 6a, top), or slightly offset, value 1 (fig. 6b, top). The initial positions of the gliders determine outcomes of their delocalisation. Glider, corresponding to the value 0 delocalised into regular identified by a symmetric pattern, like frozen waves of excitation, patterns (fig. 6a, bottom). Glider, representing the value signal value 1, delocalises into the less regular patterns (fig. 6b, bottom) identified by a non-symmetric pattern although eventually it became periodic on a long channel but not symmetric.

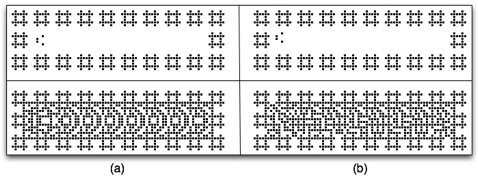
Fig. 6 Feedback channels constructed with still life patterns (a) show the initial state with the empty channel and a glider (top) and final state representing value 0 (low), and (b) show non-symmetric pattern representing value 1.

Computability in Life rule B2/S2345678 implementing a binary full adder

Implementation of final configuration of the one-bit half-adder are shown in fig. 8.

Logic gates in Life rule B2/S2345678

The patterns, representing values 0 and 1, propagate along the channels and meet at the T-junctions. They compete for the output channel, and, depending on initial distance between gliders, one of the patterns win and propagates along the output channel. This way fig. 7 shows final configurations of basic logical gates implemented in B2/S2345678.

Fig. 7 Logic gates implemented at the Life rule B2/S2345678. Input binary values A and B are represented for In/0 or In/1, output result C is represented by Out/0 or Out/1.

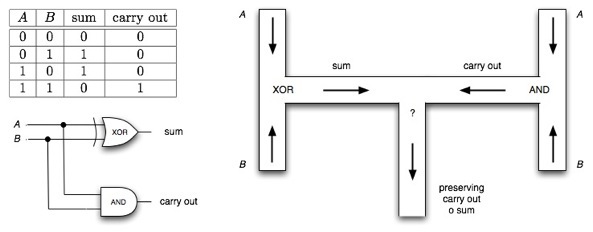
Fig. 8 Half adder circuit (left) and scheme of its implementation by propagating patterns geometrically constrained medium (right).

Implementation of final configuration of the one-bit half-adder are shown in fig. 8. Thus the circuity can be extended to a full adder (fig. 9). Configuration of the adder, outlined with Still Life blocks, and description of computation stages are shown in fig. 10. The full adder consists of 16 T-junctions, linked together by channels, and involve synchronization signals as well.

Finally the full adder was constructed on 1,118 x 1,326 cells lattice, and there were 66,630 live cells involved in 952 generations in total.

Fig. 9 Full binary adder circuit.

Fig. 10 Full binary adder serial implementation in Life rule B2/S2345678

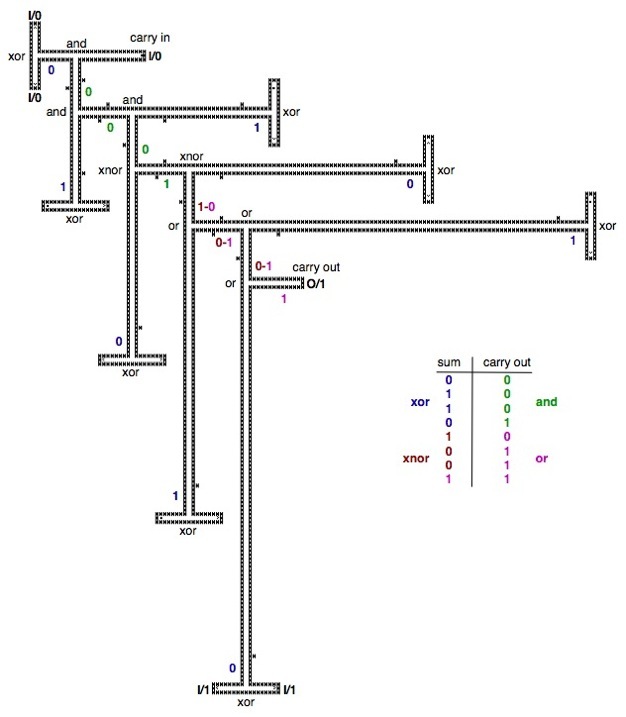
RLE files to reproduce the binary adder with the CA B2/S2345678

1. ✴Half adder in Life rule B2/S2345678 (halfAdder-2822.rle)
   

2. ✴Full adder in Life rule B2/S2345678 (fullAdder-2822.rle)
   

Contributions by Andrew Adamatzky, Harold V. McIntosh and Ben Costello.

Paper: Computation by competing patterns: Life rule B2/S2345678 [PDF]

Book: Automata 2008: Theory and Applications of Cellular Automata, Luniver Press, 2008.

University of the West of England, Bristol, United Kingdom.

Automata 2008 EPSRC Workshop Cellular Automata Theory and Applications, Bristol, United Kingdom, June 12-14, 2008.

EPSRC grant EP/F054343.