On logical gates in precipitating medium: cellular automata model

Abstract. We study a two-dimensional semi-totalistic binary cell-state cellular automaton, which imitates a reversible precipitation in an abstract chemical medium. The systems exhibits a non-trivial growth and nucleation. We demonstrate how basic computational operation can be realized in the system when the propagation of the growing patterns is self-restricted by stationary localizations. We show that precipitating patterns of different morphology compete between each other and thus implement serial and non-serial logical gates.
Constraining the media geometrically is a common technique used when designing computational schemes (particularly implementing logical circuits) in spatially extended non-linear media. For example ‘Strips’ or ‘channels’ are constructed within the medium (e.g. excitable medium) and connected together, typically using arrangements such as T -junctions. Fronts of propagating phase (excitation) or diffusive waves represent signals, or values of logical variables. When fronts interact at the junctions some fronts annihilate or new fronts emerge. They represent a result of the computation. The approach is far from being elegant (compared for instance to the collision-based paradigm) but simple and practical enough to be used by experimental scientists and engineers. This method of constraining the excitable media geometrically has enabled the design of a range of computing devices in the chemical laboratory. This has included logical gates, diodes, counters, coincidence detectors and memory all carried out using analogues of the Belousov-Zhabotinsky (BZ) medium.
In this research we investigate the possibility of computation in self-constrained reaction-diffusion systems. We develop and analize a cellular automaton model where the channels are constructed using stationary localizations and computation is implemented by propagating patterns of precipitation.
The cellular automaton
Previously we have proposed a detailed classification of two-dimensional semi-totalistic cellular automaton functions, which imitates the processes of dissociation and association in spatially extended nonlinear media. Every cell of the automaton array has eight neighbours and takes two states, 0 and 1. Cells update their states simultaneously in discrete time, depending on the sum of the states of their neighbours, and by the same cell-state transition rule. A cell in state 0 takes state 1 if the number of neighbours in state 1 belongs to the interval [θ1,θ2], otherwise the cell remains in the state 0. A cell in state 1 continue in state 1 if the number of its neighbours in state 1 belongs to interval [δ1,δ2], otherwise the cell changes the state 0. The transition parameters satisfy the following condition: 0 ≤ θ1 ≤ θ2 ≤ 8 and 0 ≤ δ1 ≤ δ2 ≤ 8. This way, the rules can be written as θ1θ2δ1δ2 .
Such a cell-state transition function can be interpreted as a simple discrete model of a quasi-chemical system with substrate ‘0’ and reagent ‘1,’ where [θ1,θ2 ] is an interval of reaction (association or precipitation), and [δ1,δ2 ] is an interval of dissociation. These family of rules includes Conway’s Game of Life (GoL), when intervals [δ,δ] and [θ,θ] are interpreted as intervals of survival and birth respectively.
We have demonstrated that this family of cellular automata is capable of constructing Voronoi diagrams, information transfer in the form of mobile self-localizations and self-development of sophisticated patterns from minimal seed conditions.
In this way, we have also discovered and verified in computational experiments that a bigger cluster of rules Life dc22, when d and c takes values of 2 to 8 and d ≤ c uniquely supports mobile self-localizations (gliders), almost frequently growing in square patterns, and complex patterns combining highly-disordered and ordered zones they are reached by initial perturbations or from reactions of mobile self-localizations; see some examples in Fig. 1.

An special attention was concentrated to develop computations in the domain of GoL with the also called “Diffusion Rule”. However common self-localizations were also involved into the big cluster dc22. In this way, a subset of rules called Life 2c22 was analyzed independently founding mobile and stationary self-localizations although they were very limited to project possible computations like in GoL. So, a significant problem was stop supernova explosions, but like was reported in an special pattern well-known as “still life” pattern in GoL, exist in 2c22. Generally, any CA that grown quickly was very complicated to stop. In this paper, we report as stop these explosions constructing “walls” in the rules 2c22 when c > 3.

Fig. 2 Enlarged photo of spiral wave-fronts in precipitating systems: copper chloride and potassium hydroxide. Size is 1 × 1mm.
Complex growing patterns generated by rule 2c22 do reflect the surprising complexity of some natural precipitating systems, where the apparent spatio-temporal dynamics is morphologically comparable to that of excitable chemical systems. A remarkable example is shown in Fig. 2. There we can see complex structures formed when certain concentrations of a simple salt, copper chloride, immobilized in thin gel sheets is reacted with a solution of potassium chloride.
Hence we construct basic computing primitives using configurations of cellular automata governed by rules 2c22. We use the propagation of waves in channels of information with stationary and mobile self-localizations. Also, we will see how processing serial and non-serial logic gates.
Computing in rules 2c22
In automata rules 2c22 we have selected the rule 2622 to made our constructions (clarity in their patterns). Of course, we could use their other four rules but it is not necessary because the other rules were just an adjustment to manipulate the same patterns, potentially all they are candidates to process the same operations and therefore proof its respective logic universality in 2c22 when c > 3.
Thus we can make an impenetrable barrier of stationary self-localizations, so-called still life configurations as we saw in previous one section. Primitively, each stationary localization is an intersection of four segments of 1 state, each segment occupies six cells in state 1; the segments intersect so to enclose the 2 × 2 domain of cells in state 0. Eventually, a family of patterns there is manipulating its width of channel and positions of mobile self-localizations. But, we have used minimum distance by mobile and stationary self-localization and it was calculated as: interval = volume still life − volume glider. Minimal space between walls limit number of patterns into of them. See exact configurations of the barrier localizations in Fig. 3.
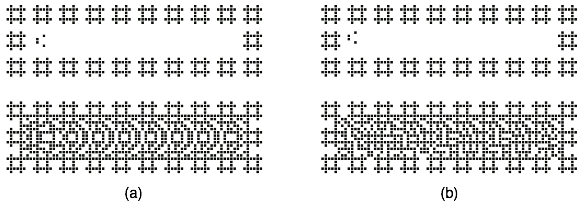
Fig. 3 Two types of patterns propagation in the information channels (bottom) and their initial configurations stimulated by a mobile self-localization (top).
Signals are represented by two types of patterns propagating along the channels (Fig. 3, bottom). Both patterns are initiated by the same localization (Fig. 3, top), consisting of four cells in state 1, but differently positioned. Logical value 0 is represented by regular wave fronts, which are generated by placing localization at the bisector of the channel’s longitudinal walls (Fig. 3a). To generate less regular patterns (representing value 1) we shift the localization one cell away from the bisector (Fig. 3b).
Truth values of Boolean variables are represented by these two propagating patterns. Computation occurs when patterns propagating in channels interact at the junctions of the channels. Configurations of cellular automata implementing the logical gates AND and OR are shown in Fig. 4. Automaton configurations before computation are shown on the left (initial state), besides you can see localizations, representing logical values 0 and 1 depending its position or phase. The configuration at the end of computation, after the patterns have completed their propagation and interaction are shown on the right in both cases.
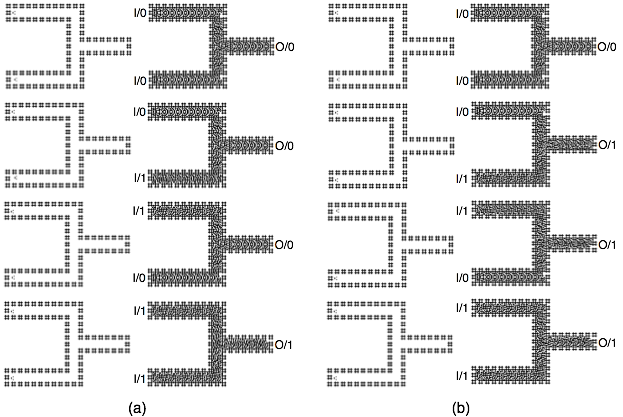
Implementation of MAJORITY gate is shown in Fig. 5. The gate has three inputs: North, West and South channels, and one output: East channel. This gate was constructed when their three propagating patterns hit in the center of the channels thus the final result (Out/?) is the result of this collisions of waves. Some similarity to construct this gates can be founded with quantum-dot cellular automata.
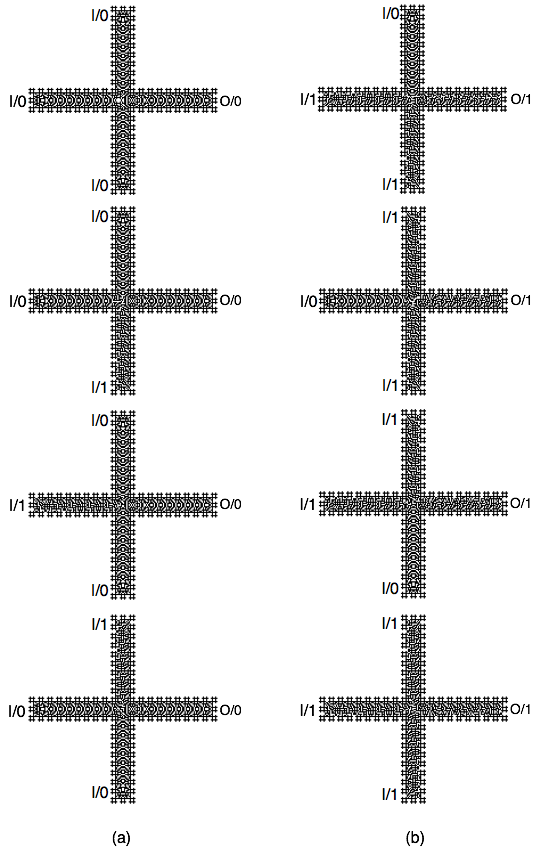
Fig. 5 Cellular automaton implementation of MAJORITY gate: (a) all cases corresponding to majority input value In/0, (b) all cases corresponding to majority input value In/1.
The computation in the 2c22 medium is based on competition between two types of propagating patterns. We believe the theoretical results discussed will demonstrate their practical value in experimental implementations of geometrically constrained non-linear medium processors, chemical processors and self-growing nano-structures.
Implementations and constructions were are done with Golly system. RLE files to reproduce all simulations with the CA B2/S23456 are.

Contributions by Andrew Adamatzky and Ben Costello.
Paper: On logical gates in precipitating medium: cellular automata model [PDF]
Journal: Physics Letters A 1(48), 1-5, 2008.
University of the West of England, Bristol, United Kingdom.
Supported by Engineering and Physical Sciences Research Council (EPSRC), United Kingdom, grant EP/F054343.